Архитектон: известия вузов. №3 (91) Сентябрь, 2025

Теория архитектуры

Эталон фасада деревянного дома

УДК: 72.01
Шифр научной специальности: 2.1.12
DOI: 10.47055/19904126_2025_3(91)_5

Аннотация

… нет красоты и удовольствия без пропорции,
а пропорция должна быть найдена прежде всего в числах;
все вещи должны иметь числовую пропорцию…
число является главным образцом в уме Творца, средством,
которое в вещах ведет к мудрости».
Из сочинения Бонавентуры «Itinerarium mentis in Deum», XIII век

То, что мы называем арифметикой,
Боэций назвал бы логистикой.
В Средние века арифметика в нашем понимании
была известна как алгоритмизм.
den Hartog, E., 2014

Когда теория совпадает с эксперементами,
это уже не открытие, а закрытие.
Петр Леонидович Капица (1894–1984)

Введение

Народное деревянное зодчество приволжских районов Горьковской области отличается высокими художественными достоинствами и ярко выраженным своеобразием. Развивая традиции русского зодчества, народные мастера последовательно осуществляли свои замыслы до самой мелкой архитектурной детали, создавали оригинальные образцы декоративного убранства, подчеркивающего композиционные и технические особенности деревянной архитектуры [1,4,7–13].

Наиболее распространенный тип жилых сооружений в Горьковской области – одноэтажный дом клетью, план которой приближается к квадрату. Такие дома составляют основную массовую застройку российских деревень конца XVIII – первой половины XIX в.

Немногочисленность композиционных и конструктивных приемов, применявшихся строителями крестьянских жилых домов, была следствием отбора лучших практик, которые становились общепринятыми и повторялись, постепенно совершенствуясь и видоизменяясь в течение десятилетий и даже столетий. Такие дома обладают исключительной продуманностью и законченностью, выверенностью общей композиции фасадов и отдельных элементов, органическим единством резного декора и архитектуры. Народные мастера полностью подчиняли композиции сооружения его орнаментальное убранство, что вряд ли возможно без владения ими рациональными приемами организации фасада, в которых мы видим красоту, предугадывая меру. Однако при всей красоте объектов деревянного зодчества рациональные принципы его формообразования остаются нераскрытыми.

В этой связи представляется важным проверить на эталонных образцах формообразующую роль принципов кратности и архитектурной ординации, обнаруженные и сформулированные нами ранее [6]. Среди них, прежде всего, надо выделить свойства средней и крайней пропорции с единым коэффициентом ординации, а также принцип кратности габаритных размеров фасадов и величин гармоник протяженностей, присутствующих в элементах фасадов.

Цель статьи – на примере эталонного фасада деревянного дома раскрыть в первом приближении принцип кратности, регулирующий размерную взаимосвязь общих габаритов фасада (ширина, высота) и его частей (окон, простенков, наличников, рам, фризов, причелин, декоративных обрамлений и т. д.). Предполагается достигнуть поставленной цели решением следующих задач:

1) выполнить ординационный анализ эталонного фасада жилого дома, направленный на выявление количественных характеристик его архитектурного строя;
2) определить доминирующий архитектурный строй для вертикальных и горизонтальных членений эталонного фасада;
3) установить кратную размерную взаимосвязь общих габаритов фасада и его элементов;
4) дать определение принципа кратности, характеризующего соразмерность структурных элементов фасада.

Гипотеза исследования в рамках статьи заключается в предположении существования кратной размерной корреляции общих разновеликих габаритов эталона фасада деревянного дома и его архитектурных деталей.

Метод исследования в рамках статьи связан с установлением величин протяженности общих разновеликих габаритов фасада и кратных им размеров элементов фасада, после чего определяется доминирующая и прочие кратности.

Использованные в статье термины и определения.

Эталон фасада деревянного дома – ортогональное изображение фасада деревянного дома, выбранное из множества подобных для проведения анализа размерных параметров общих и локальных габаритов целого и его частей.

Общие габариты фасада деревянного дома – его максимальная высота и ширина. Локальные габариты – размерные характеристики по вертикали и горизонтали отдельных элементов и их частей.

Гармоники горизонтальной и вертикальной протяженностей – это цельнократные общим габаритам по вертикали или по горизонтали протяженности локальных габаритов или размеров элементов фасадов;

Ордината – графический маркер в виде стрелок и точек, обозначающий на чертеже архитектурного объекта его структурные элементы, находящиеся в отношении крайнего или среднего деления.

Коэффициент ординации, Корд – количественная характеристика, число, фиксирующее отношение крайнего ((М+m)/М) или среднего (М:m) деления частей отрезка А на две неравные части: М и m.

Кратность – число Р, показывающее во сколько раз одна протяженность больше другой.

Пропорциональные диспозиции – образующиеся при разделении отрезка А на две неравные части М и m варианты диспозиций сравниваемых величин (всего 9 вариантов), среди которых в теории архитектуры преобладают два: средняя пропорция и крайняя пропорция.

Средняя пропорция деления отрезка А на две неравные части «М» (большую) и «m» (меньшую) – это отношение М:m. В изображении ординатой средней пропорции это выглядит так:

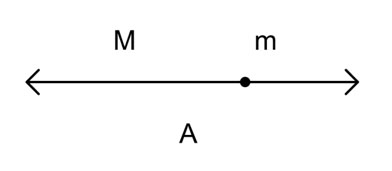
где А – весь делимый отрезок,
М – большая часть разделенного отрезка А,
m – меньшая часть разделенного отрезка А.

Крайняя пропорция деления отрезка А на две неравные части «М» (большую) и «m» (меньшую) – это отношение А:М. В изображении ординатой крайней пропорции это выглядит так:

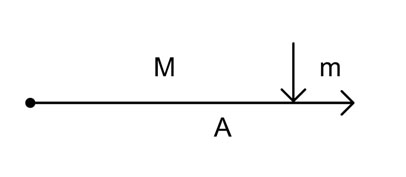
Кратность (величина Р) крайней пропорции деления отрезка А на две неравные части: М и m существует в 3-х величинах: Р_а, Р_м, Р_m. Все они должны быть целочисленными Р_а=А:m; P_м=M:m; Р_m=m:m=1; P_а=Р_м+Р_m=P_м+1. Отсюда следует, что «m» является размерной единицей всех величин крайнего пропорционального разделения отрезка А.

Кратность (величина F) средней пропорции деления отрезка А на две неравные части: М и m существует в 3-х величинах: F_a=A(M-m); F_м=M:(M-m); F_m=m:(M-m);

При этом F_a= F_м+F_m, а размерной единицей является величина (М-m)=1.
Все величины кратности F – целые числа.
Величины А, М, m могут быть выражены в целых единицах, равных (М-m).

Преобразованная ордината среднего пропорционального деления используется для наглядного изображения размерной единицы кратности.

Исходная ордината среднего пропорционального деления выглядит так:

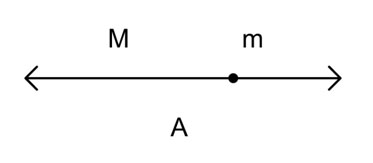
Преобразованная ордината среднего пропорционального деления выглядит так:

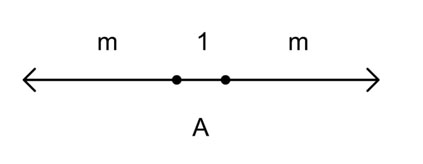
поскольку М=m+1.

Забегая вперед, отметим, что очень часто при помощи преобразованной ординаты среднего пропорционального деления определяются габариты и местоположение центральных элементов фасадов и их частей: окна или портала, осей простенков и окончин, ширины среднего импоста оконной рамы и т.д.

Целочисленная кратность протяженностей – соотношение деления большей и меньшей протяженностей, равное целому натуральному числу;

Доминирующая целочисленная кратность протяженностей элементов фасада – наиболее часто повторяемая кратность, характеризующая соотношение общих габаритов фасада с локальными.

Разноразмерные общие габариты сруба деревянного дома – это совокупность следующих размеров:

1) ширина сруба, равная длине его поперечных бревен (В1);
2) максимальный горизонтальный габарит по внешнему контуру торцов бревен сруба (В2);
3) расстояние между внешними крайними точками продольных пазов выпусков торцов бревен сруба (В3);
4) расстояние между осями торцов сруба (В4);
5) расстояние между внутренними крайними точками продольных пазов выпусков торцов бревен сруба (В5);
6) внутренний габарит между выпусками торцов бревен сруба (В6); он же ширина прясла сруба (рис. 1).

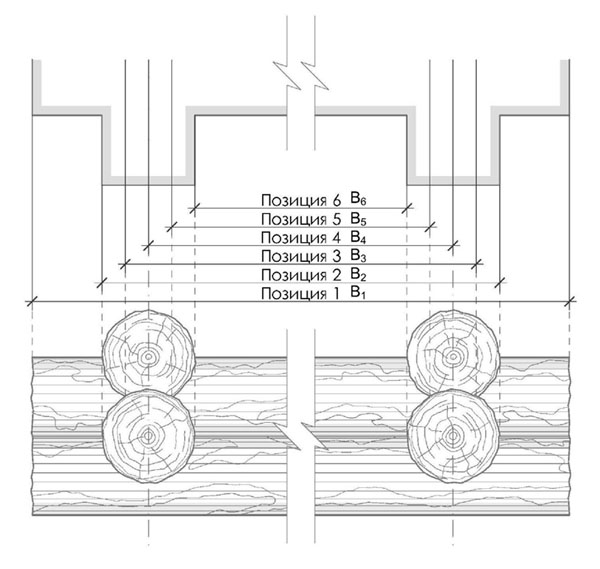
Рис. 1. Разноразмерные общие габариты сруба деревянного дома. Автор: А.В. Долгов, чертеж: А.Д. Бурганов

протяженность – расстояние между крайними точками общего или локального габарита;

гармоники протяженности – цельнократные части какой-либо протяженности;

поликратные гармоники – совокупность гармоник протяженностей разных целочисленных кратностей по отношению к какой-либо протяженности, выделяемой на фасаде.

Введение в терминологию статьи нового для теории архитектуры категории «гармоника протяженности» базируется на понятной аналогии с гармониками в теории музыки [14,15].

Представленные выше соображения позволили нам выбрать в качестве анализируемого эталона фасад дома Авакимовых в Городце (рис. 2).

Рис. 2. Дом Авакимовых в Городце. Главный фасад [7, табл. 4]

Рассмотрим, проявляется ли какая-либо кратность в качестве основной, моделирующей размеры фасада в общих габаритах и в деталях. Памятуя о пословице «семь раз отмерь, один раз отрежь», начнем с кратности Р=7 и привяжем к ней ординаты средней и крайней пропорции, согласно авторскому графо-аналитическому методу архитектурных ординат. При кратности 7 мы понимаем, что M:(М-m)=7, К_орд = М/m = 7/6.

Перейдем к анализу проявления кратности 7 на фасаде, выбранном в качестве эталона (рис. 3).

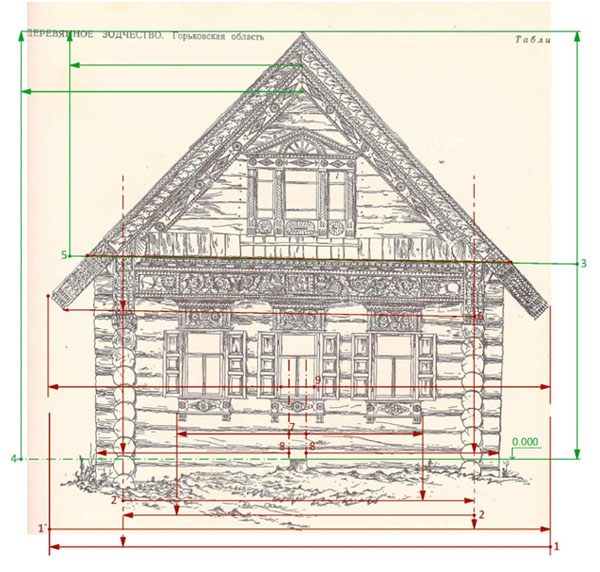
Рис. 3. Проявление кратности 7 в моделировании форм фасада эталонного деревянного дома Авакимовых из Городца [7, табл. 4]

1. Ординаты 1 и 1ʹ Обнаруживают кратность 7 в отношении размера между крайними точками размаха причелин (самый протяженный горизонтальный габарит на фасаде) к расстоянию от крайней точки причелины до ближайшей к ней оси торцов выпусков бревен (оси сруба).

2. Ординаты 2 и 2ʹ выявляют кратность 7 в отношении расстояния между осями поперечных стен сруба и расстоянием от оси сруба до ближайших к ним элементов оконных наличников. Тем самым на фасаде выделяется габарит, в границах которого размещается 3-оконная группа наличников.

3. Ордината 3 привязана к условной нулевой отметке на фасаде дома, намеченной на чертеже высотой пенька (очевидно, введенного в изображение в качестве подсказки). Верхняя часть ординаты как 7:6, фиксирует отметку нижнего края слива фронтона, которая делит весь фасад по вертикали на две части: сруб и фронтон – щипец.

4. Ордината 4 выявляет на фасаде общую высоту венчающего фронтона резного декора, состоящего из двух частей: причелины и накладной наклонной доски контура фронтона. Кратность 7 = высота всего дома от условной нулевой отметки до конька щипца – фронтона, поделенная на высоту декоративного завершения фронтона и причелин щипца.

5. Ордината 5 обнаруживает кратность 7 как соотношение высоты треугольника фронтона (от нижней границы слива до конька) к высоте стыка причелин.

6. Ордината 6 выявляет кратность 7 в отношении расстояния от нижней точки причелины до правой (дальней) оси сруба к размеру от края левой причелины до левой оси поперечной стены сруба.

7. Ордината 7. В границах общего габарита ширины 3-оконной группы определяет местоположение осей вертикальных окончин рамы среднего окна с использованием кратности 7.

8. Ордината 8 и 8ʹ связывают кратностью 7 расстояние от осей вертикальных окончин среднего окна до краев выпусков поперечных бревен с расстоянием от оси продольных бревен сруба до краев выпусков поперечных бревен.

9. Ордината 9 связывает кратностью 7 внутренний (остекленный) размер ширины оконной рамы и общую ширину размаха причелин по крайним точкам.

Отмеченные кратности 7 лишь часть из их общего количества, которые можно с очевидностью обнаружить на фасаде дома, что будет показано на последующих примерах. Найденные соразмерности, связанные с кратностью 7, неотделимы от соразмерностей, определенных через коэффициент ординации равный 7:6. В связи с этим обращает на себя внимание еще одна подсказка мастера, строившего и украшавшего дом. Она заключается в количестве капель на правом и левом концах причелин. У левой причелины их 6, а у правой 7.

Перейдем к ординационным и кратным соотношениям, основанным на кратности 7 в деталях фасада (рис. 4), чтобы убедиться в их моделирующей форму роли.

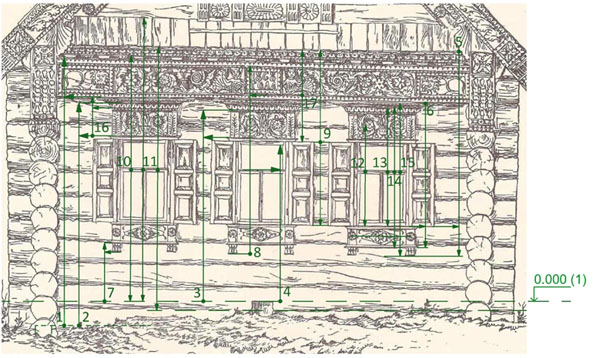
Рис. 4. Вертикальные ординаты, проявляющие моделирующие свойства кратности 7
в формообразовании декоративных элементов фасада деревянного эталонного дома Авакимовых из Городца

Вертикальные ординаты:

Ордината 1. Ее основание находится ниже условной нулевой отметки ввиду того, что дом расположен на небольшом склоне и самое нижнее продольное бревно сруба уходит в землю. Однако нам известно, что отметки сруба считают по уровню опорной площадки замка окладного венца (нижнего продольного и поперечного бревен). На рис. 4 этот ноль обозначен пунктиром в нижнем торце нижнего бревна в уровне (•) 1 и 2. Обычно окладной венец состоит из двух нижних продольных и двух поперечных бревен. Таким образом, отметки условного нуля (верх пня) и уровня замковой площадки отличаются друг от друга ровно на высоту венца сруба. По этой причине у срубной конструкции может быть, если так можно выразиться, два нуля (нижний и верхний). В нашем случае нижний ноль находится на уровне точек 1 и 2, а верхний – на уровне точек 3, 4, 7.

Именно к уровню нижнего нуля привязана ордината 1, которая помогает нам увидеть, что высота резной фризовой доски равна 1/7 всей протяженности ординаты 1.

Ордината 2. Начинается на уровне нижнего нуля и позволяет определить кратную ей высоту лобовой доски оконного наличника с резным карнизом поддерживающего профиля, на котором покоится протяженная венчающая резная доска высотой в 1/7 ординаты 16.

Ордината 3. Ее начало находится на отметке условного (верхнего) нуля. Ордината проявляет тот факт, что высота лобовой доски оконного наличника ровно в 7 раз меньше протяженности ординаты 3.

Ордината 4 ясно показывает, что высота горизонтальной окончины равна 1/7 длины ординаты 4, которая начинается на отметке верхнего нуля.

Ордината 5 наглядно выявляет, что высота подоконной доски наличника вместе с серьгами (каплями) ровно в 7 раз меньше ординаты 5.

Ордината 6 показывает, что высота подоконной доски без серег (капель) равна 1/7 высоты всего наличника без серег (капель).

Ордината 7 привязывает высоту серег (кистей) наличника под подоконной доской к отметке условного (верхнего) нуля в отношении 1 к 7 протяженности ординаты 7.

Ордината 8 наглядно раскрывает венчающую роль декора фризовой доски и таблички с датой по отношению к уровню нижней отметки начала декоративных элементов фасада (низ серег лент наличника).

Ордината 9 помогает увидеть соотношение 7 к 6 в высоте ставен и расположенного над ними двухчастного пояса резьбы (навершие наличника + фризовая доска с подзорами карниза).

Ордината 10 проясняет местоположение горизонтальной среднепропорциональной линии прясла фасада, заключенной между низом карнизного выноса и условной (верхней) нулевой отметкой. Нижняя часть ординаты относится к верхней как 7 к 6.

Ордината 11. Так же, как и ордината 10, закрепляется на среднепропорциональной горизонтальной линии фасада, проходящей по границе обрамления верхней горизонтальной окончины и нижними открывающимися двойными створками оконной рамы. Она наглядно закрепляет соотношение 7 к 6 в границах низа тимпана фронтона и условной (верхней) нулевой линии.

Ординаты 12, 13, 14, 15 проявляют среднепропорциональные отношения 7:6 в композиции окна и его наличника.

Таким образом, обозначенные на фасаде ординаты крайнего и среднего пропорционального разделения, позволяющие увидеть на фасаде совокупность соразмерных протяженностей, связанных кратностью 7 или коэффициентом ординации, равным отношению 7 к 6, подтверждают их моделирующую роль в системе вертикальной размерности строя фасада деревянного дома, принятого за эталон.

Система горизонтальных линейных гармоник в размерной зависимости от основных габаритов фасада (рис. 5)

В ходе нашего исследования, кроме того, что мы выявили моделирующую роль кратности 7, возникла гипотеза о том, что ее должны сопровождать иные кратности, привязанные к существующим и отчетливо воспринимаемым общим габаритам бревенчатой стены. Глазу невозможно объяснить, что какие-то воспринимаемые габариты надо считать главными, а какие-то – второстепенными. При восприятии очевидно только то, что одно больше или меньше другого.

Нами уже было показано, что в системе общих габаритов бревенчатой стены существует 6 позиций, отличающихся размерно, но не ранжированных по главенству восприятия. В этом заключается одна из важнейших особенностей деревянного зодчества, заданная априори особенностями конструкций угла здания, допускающей полимерность исходных размерных габаритов, что, несомненно, должно отражаться в элементах организации фасада внутри прясла.

В связи с этим установленные нами ранее зависимости линейных размеров оконных прорубов, колод, наличников, подтверждая принципы кратной соразмерности с габаритами, не позволяют игнорировать сложность ситуации, пытаясь ее упростить. Наверняка от упрощения и грубой схематизации пропадет что-то очень важное, а может быть, и главное – принцип достижения гармонии и баланса форм фасадов деревянных домов, следование которому позволяло достигать высокого эстетического качества. Многие десятилетия, характеризуя фасады традиционных массовых типов домов, кроме указания количества окон на фасаде, ни о какой детерминации форм в общей композиции фасада не было и речи. Получалось, что собственно архитектурный анализ внешних форм домов отсутствовал, подменяясь совокупностью описания видимых форм.

Поликратные гармоники протяженностей наряду с использованием аналитического инструментария архитектурной ординации и кратности еще никогда не применялись. Поэтому очень важно апробировать на эталонном фасаде анализ зависимости поликратных гармоник протяженностей от полимерных общих габаритов прясел деревянных домов.

Важно изначально понимать, что аналитический метод архитектурных ординат способен установить доминирующую кратность и коэффициент ординации. Именно они и отвечают за моделирование исходной структуры фасада, которая, словно игрушками на елке, должна быть заполнена поликратными гармониками протяженности, представленными на фасаде.

Попробуем в самом первом приближении представить аналитическую схему обнаружения на фасаде горизонтальных линейных гармоник, полученных от (для начала) четырех исходных габаритов фасада (AB, CD, EF, MN).

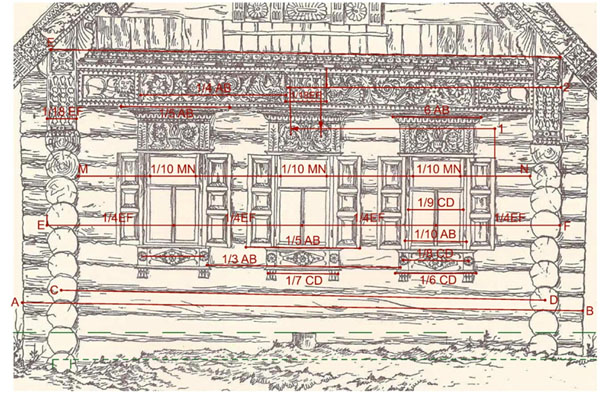
Рис. 5. Горизонтальные линейные гармоники в размерной зависимости от основных габаритов фасада

Мы видим, что даже отмеченных гармоник протяжности, каждая из которых имеет конкретную пару в габаритном размере прясла, довольно много и они весьма разнообразны. Каждая пара может стать моделирующей для всего фасада через определенный алгоритм применения конкретной кратности. Из них следует выбрать наиболее рациональный и понятный, что довольно сложно: ведь критерий отбора подходящего алгоритма нам неизвестен. Сами цифровые комбинации его не проявляют.

Но, поскольку мы имеем дело с архитектурной композицией, то в состоянии сформировать желаемую установку на поиск алгоритма, который мог бы связать визуальным подобием и кратностью части и целое. Например, горизонтальные протяженности общих габаритов прясла и структурные элементы окна в их горизонтальных размерах, т. е. установить размерно-композиционную корреляцию в масштабах кратности.

Нами была проведена работа по подбору оптимального моделирующего алгоритма для разных кратностей: от 5 до 16. Как и ожидалось, наиболее подходящей стала кратность 7, связавшая очевидными цепочками композиционно-размерного подобия структуры окна и общие размерные характеристики фасада, начиная от размаха причелин, коррелируемого с шириной венчающего карниза, и заканчивая парой – размер между левой и правой границей стекла на фасаде и шириной стекла в оконной раме центрального окна. Далее коррелируемые кратностью 7 размерные пары выглядят так:

1. Протяженность фасадной стены сруба/длина горизонтальных профилей, выступающих за границы ширины наличника = 7.
2. Расстояние между внешними границами выпусков бревен прясла/ширина оконного наличника = 7.
3. Расстояние между осями торцов бревен прясла/ширина оконной колоды = 7.
4. Ширина прясла между выпусками бревен/расстояние между открытыми ставнями в створе окна = 7.
5. Ширина оконной группы по габариту распахнутых ставен/ширина оконной рамы = 7.
6. Расстояние между крайними осями петель ставен 1-го и 3-го окна/ширина остекленной части верхней окончины = 7.
7. Расстояние между правой и левой границами оконных рам 1-го и 3-го окна/ширина остекления двустворчатой части оконной рамы = 7.
8. Локальные проявления кратности 7 представлены на иллюстрациях.

Интересно, что практически те же размеры основных горизонтальных протяженностей элементов окна с наличником мы можем получить через кратность10, двигаясь от периферии к центру.

1. Расстояние между верхними точками краев причелин/ширина оконной колоды = 10.
2. Расстояние между нижними точками краев причелин/ширина оконного проруба = 10.
3. Ширина бревенчатого фасада/расстояние между ставнями в створе окна = 10;
4. Ширина прясла по наружным габаритам выпусков бревен/ширина оконной рамы = 10.
5. Ширина прясла между выпусками бревен по внутреннему габариту / ширина стекла в раме окна = 10.
Другие кратности, например 5, 6, 8, 9 не доминируют в получении наиболее характерных размеров окна, связанных с общими габаритами фасада, но также участвуют в наполнении его пластики своими гармониками, фиксируемыми в материале как архитектурные или декоративные элементы. Тем самым образуется полный спектр возможных гармоник, участвующих в формировании структуры и декоративном наполнении фасада, лишая его сухости и схематизма, придавая ему живые черты и характер.

Очевидно, с этим связано ощущение слитности и нерасчлененности композиционного результата, наполненного еще и многообразными смыслами изобразительного фольклора, что так свойственно народному искусству и более всего в современной искусствоведческой мысли определяется категорией синкретизм.

Заключение

Таким образом, выбранный нами для композиционно-метрологического анализа эталон фасада деревянного дома не только подтвердил последовательно формулируемые гипотезы исследования (от размерного ядра до поликратных гармоник протяженностей), но и показал свою безусловную принадлежность к высоким образцам народного искусства, которых в нашем отечестве множество, однако их достоинства изучены еще крайне мало.

Известно, что в массовой строительной практике измерительный инструмент народного мастера был довольно скуп и специфичен. Главную роль в нем играл отбивочный (он же разметочный) шнур со скользящими узелками. На нем не откладывались ни сажени, ни метры, ни аршины, ни вершки, так как это мешало бы в процессе работы его универсальному применению, связанному с получением кратных величин (размеров) производных от общих габаритов сруба путем сложения согласно требуемой кратности. Кратность задавалась числами от 2 до 12 с добавлением 16 и 18. В этой цепочке различных кратностей доминирует кратность 7, а также связанные с ней через единицу, сопутствующие кратности 6 и 8, т.е. 7 + 1=8; 7 – 1=6. Такой принцип справедлив и для других кратностей, не равных 7, но также встречаемых на практике. Например, кратность 5 имеет сопутствующие кратности 4 и 6, а кратность 3, соответственно, 2 и 4.

Получаемые при этом размеры, фиксирующие габариты частей или элементов фасадов, мы назвали гармониками протяженностей и их кратных частей, которые в совокупности образуют лады гармоник протяженностей или слаженных протяженностей, которые обеспечивают формирование консонансных размерных интервалов структуры фасадов по вертикали и по горизонтали.

Поражает и заставляет задуматься о художественном гении русского народа и тот факт, что такой синкретический подход в домостроительстве был повсеместным, став идейной и художественной основой массового жилищного строительства конца XVIII – первой половины XX в. Ничего подобного мы не находим в современном массовом жилищном строительстве, отказавшемся из-за неведения от всего положительного, что можно бы было позаимствовать в традиционном зодчестве, да так и не создавшем высоких эстетических образцов массового жилища.

Библиография

1. Бодэ, А.Б. Русское народное зодчество. Произведения народных мастеров и вековые традиции / А.Б. Бодэ. – М.: Северный паломник, 2012. – 670 с.

2. Витрувий Поллион. Об архитектуре. Десять книг. Пер. с лат. / Ред. и введение А.В. Мишулина / Витрувий Поллион. – Л.: Соцэкгиз. Ленингр. отд-ние, 1936. – 341 с.

3. Гельмгольц, Г. Учение о слуховых ощущениях как физиологическая основа для теории музыки / Г. Гельмгольц. – СПб., 1875. – 590 с.

4. Долгов А.В. Деревянное зодчество Урала. Свердловская область. Челябинская область / А.В. Долгов, Н.Н. Митина, В.Д. Оленьков. – Екатеринбург: Сократ. 2012. – 232 с.

5. Долгов, А.В. Доминирующее отношение линейных параметров Парфенона А.В. Долгов // Академический вестник УралНИИпроект РААСН. – 2017. – № 4. – С. 45–49.

6. Долгов, А.В. Принцип кратности в формировании фасада деревянного жилого дома / А.В. Долгов // Архитектон: известия вузов. – 2024. – № 4 (88).– URL:  https://archvuz.ru/2024_4/8/

7. Ковальчук, Н.А. Деревянное зодчество. Горьковская область / под ред. Д.П. Сухова и П.Н. Максимова. – М.: Гос. изд-во лит-ры по строительству и архитектуре, 1955.

8. Лисенко, Л.М. Дерево в архитектуре / Л.М. Лисенко. – М.: Стройиздат, 1984. – 176 с.

9. Маковецкий, И.В. Архитектура русского народного жилища / И.В. Маковецкий. – М.: Изд-во АН СССР. Институт истории искусств, 1962. – С 16. Табл. 32

10. Мачинский, В.Д. Крестьянское строительство в России / В.Д. Мачинский. – М.: Новая деревня, 1924. – С. 5–36.

11. Митина, Н.Н. Дом из Лучинкино / Н.Н. Митина. – Екатеринбург : Региональная студия ra 4. ru, 2010. – 192 с.

12. Ополовников, А.В. Сокровища Русского Севера / А.В. Ополовников.– М. : Стройиздат, 1989. – 366 с.

13. Орфинский, В.П., Гришина, И.Е. Традиционный карельский дом / В.П. Орфинский, И.Е. Гришина. – Петрозаводск : Изд-во Петрозавод. гос. ун-та, 2009. – 478 с.

14. Сакральная геометрия, нумерология, музыка, космология, или квадривиум: от Пифагора до наших дней / Дж. Мартино, М/ Ланди, Дж. Мартино и др. ; [пер. с анг. М.С. Мкргычевой]. – М. : Эксмо, 2015. – 416с. : ил. – (Золотой фонд эзотерики).

15. Учебник гармонии / И. Дубовский, С. Евсеев, И. Способин, В. Соколов. – М., Музыка, 2012. – 480 с.: нот.

Ссылка для цитирования статьи

Долгов, А.В. Эталон фасада деревянного дома / А.В. Долгов //Архитектон: известия вузов. – 2025. – №3(91). – URL: http://archvuz.ru/2025_3/5/  – DOI: https://doi.org/10.47055/19904126_2025_3(91)_5 

Лицензия Creative Commons
Это произведение доступно по лицензии Creative Commons "Attrubution-ShareALike" ("Атрибуция - на тех же условиях"). 4.0 Всемирная